Basic Quantum Computing - Single Qubit Systems

We’re finally ready to start getting into some actual quantum computing. In our last post, we introduced the qubit. This was a quantum state of the form:

\[a\ket{0} + b\ket{1}\]

We said that it evolves in time according to some unitary matrix U.

In Quantum Computing, there is the idea of a quantum gate, which acts on a qubit. Just like a regular logic gate acts on a classical bit. Now a quantum gate changes a quantum state so it must be represented by a unitary matrix.

In this post, we’ll take a look at a couple of common gates that work on a single qubit.

The NOT Gate

Just like in classical computing, we have a NOT gate. This takes a qubit and sends 0 to 1 and visa versa. So if I have:

\[a\ket{0} + b\ket{1}\]

Applying a NOT gate to it gives me:

\[a\ket{1} + b\ket{0} = b\ket{0} + a\ket{1}\]

Because we can represent a qubit as a column vector:

\[a\ket{0} + b\ket{1} = \begin{bmatrix}a \\ b \end{bmatrix}\]

We can represent the NOT gate by the matrix:

\[\begin{bmatrix}0 & 1 \\ 1 & 0\end{bmatrix}\]

In a diagram we use the following symbols for it:

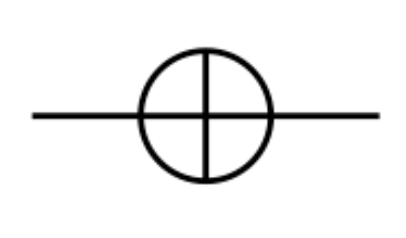
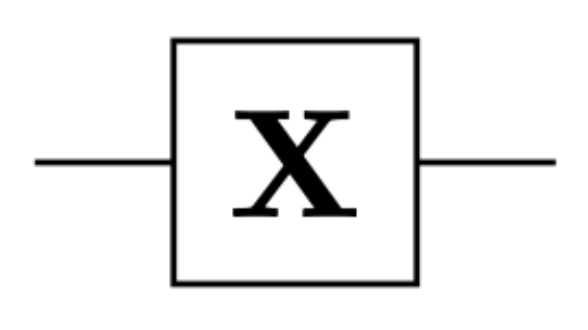
This gate is also known as the X gate because it is part of a family of three gates with the others called the Y and Z gates.

Pauli Gates

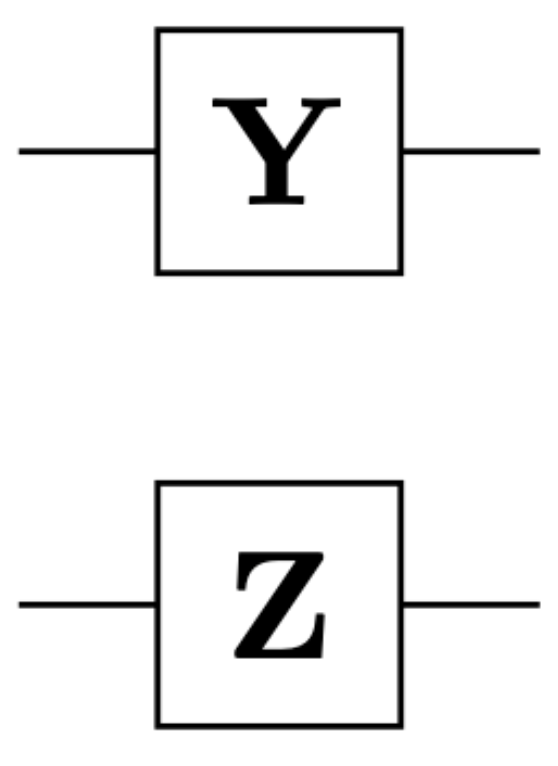
The other two gates that are in the same family as the NOT gate are the Y and Z gates. And they are given by the following matrices:

\[Y = \begin{bmatrix}0 & -i \\ i & 0\end{bmatrix}\] \[Z = \begin{bmatrix}1 & 0 \\ 0 & -1\end{bmatrix}\]

And we use the following symbols for it:

Hadamard Matrix

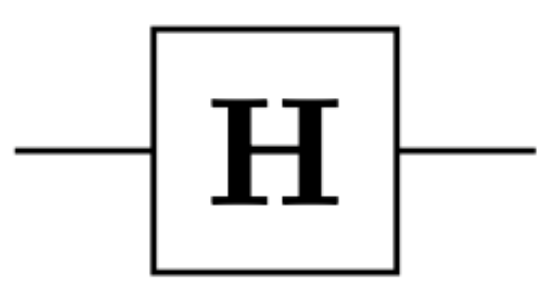
Finally, we are going to talk about the Hadamard gate. The Hadamard gate does the following:

\[\ket{0} \to \frac{\ket{0} + \ket{1}}{\sqrt{2}}\] \[\ket{1} \to \frac{\ket{0} - \ket{1}}{\sqrt{2}}\]

At first, having a gate that does this might seem rather strange but it is in fact incredibly useful. This is because it allows us to put qubits into a state where they are equally likely to be 0 or 1.

It is represented by the matrix:

\[\frac{1}{\sqrt{2}}\begin{bmatrix}1 & 1 \\ 1 & -1\end{bmatrix}\]

And we use the following symbol for it: