Basic Mathematics For Quantum Mechanics - Exponential Form of Complex Numbers

Last time, we talked about complex numbers as numbers of the form a + bi where i is the square root of -1. This is true but there is another way of writing them which is sometimes more helpful.

Polar Form

Let’s start by recalling the argand diagram where we plot the real part of the x-axis and the imaginary part on the y-axis.

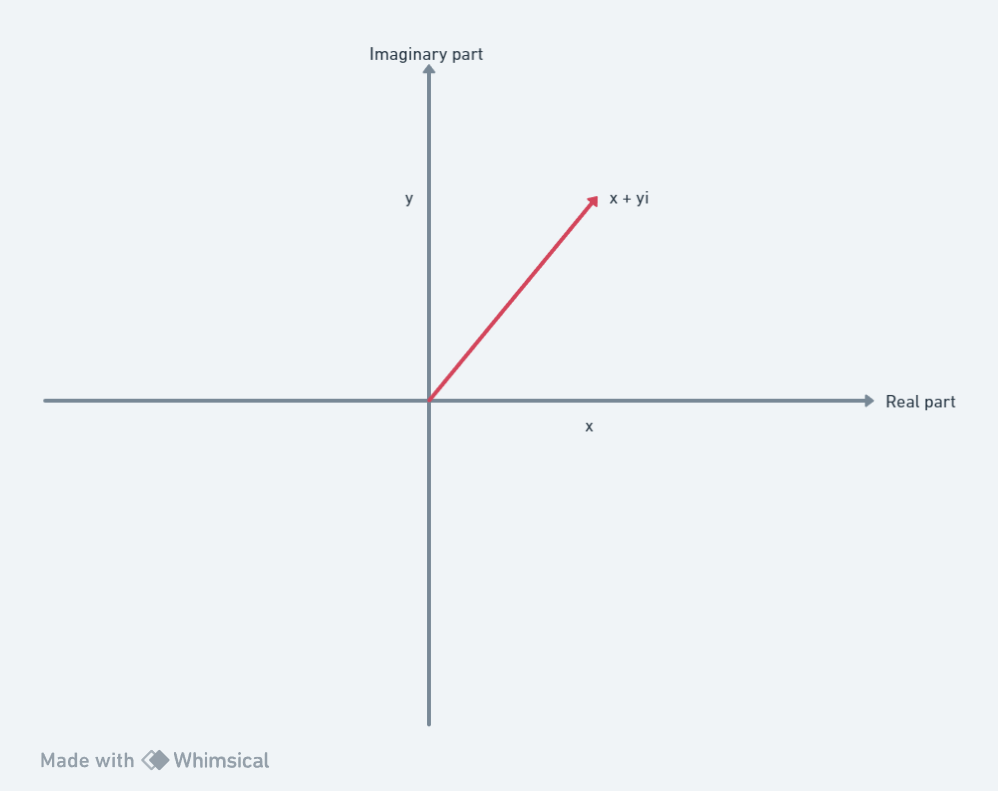
Here the complex number is represented by an arrow. You might remember from school that there is another way of describing arrows.

We can describe an arrow by how long it is and what (anticlockwise) angle it makes to the positive x-axis. The length of the arrow is shown in the picture by the letter r and the angle is denoted by the letter t

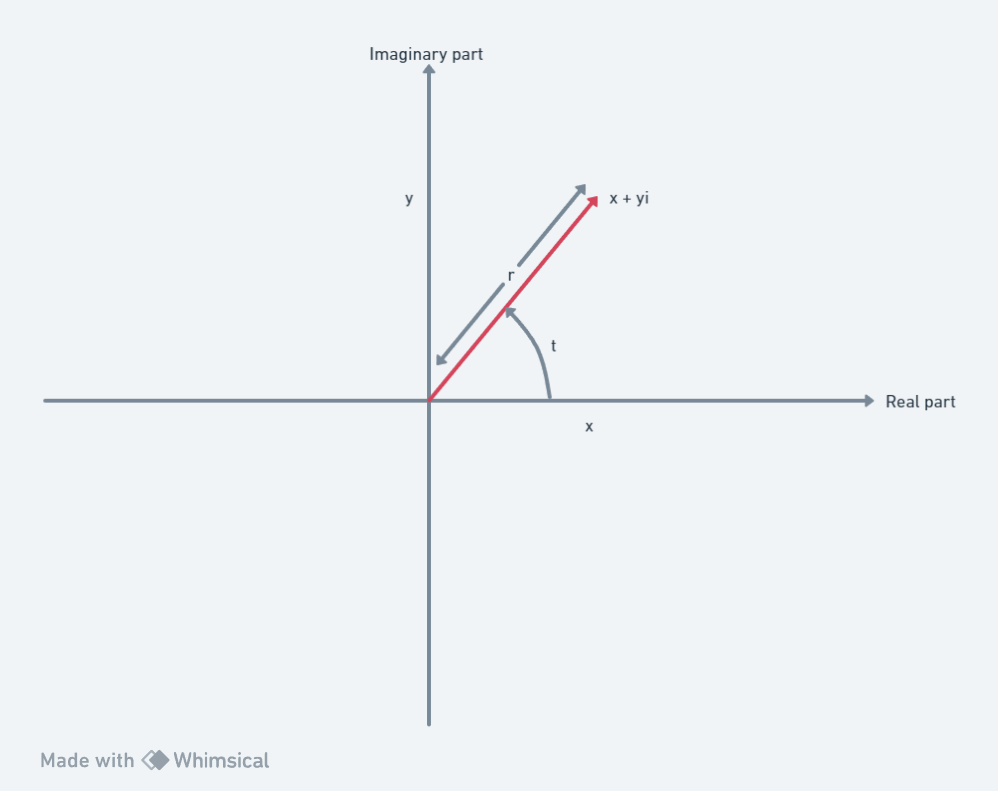
So we can write a complex number as a pair of numbers (r, t) where r is the length and t is the angle.

r and t have special names. r is called the modulus of the complex number and t is called the argument.

Given a complex number in polar form so we have a radius and an angle we can use a bit of high school trigonometry to find that:

\[a = r cos(t)\] \[b = rsin(t)\]

So putting this together we can write a complex number as

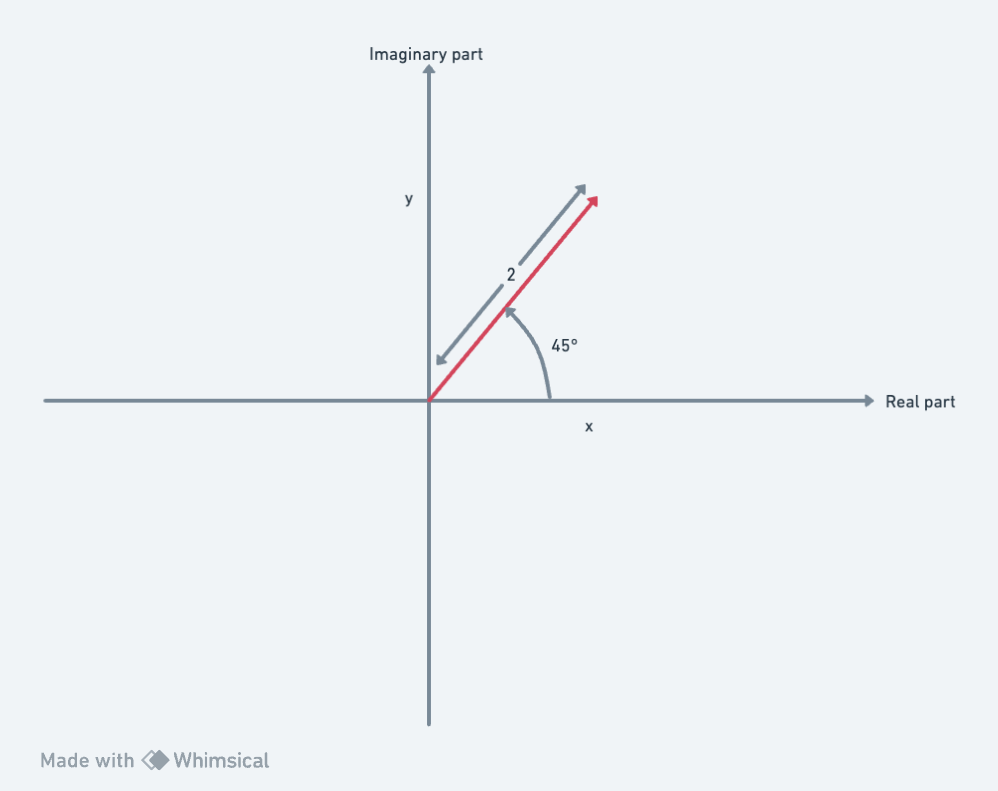
\[a + bi = rcos(t) + irsin(t) = r(cos(t) + i sin(t))\]

To see this let’s look at an example. Consider the following number of radius 2 and that makes an angle of 45 degrees to the axis.

Well we know that

\[cos(45) = sin(45) = \frac{\sqrt{2}}{2}\]

So we get

\[a = b= 2 * \frac{\sqrt{2}}{2} = \sqrt{2}\]

So

\[z = (2, 45) = \sqrt{2} + \sqrt{2}i\]

Finding the modulus and argument

The modulus of a complex number z = a +bi is demoted by |z| and it has a simple formula :

\[|z| = \sqrt{a^2 + b^2} = z\overline{z}\]

The argument also has a simple formula given by

\[arg(z) = tan^{-1}(b/a)\]

To see this in action let’s do an example.

Let’s take the number:

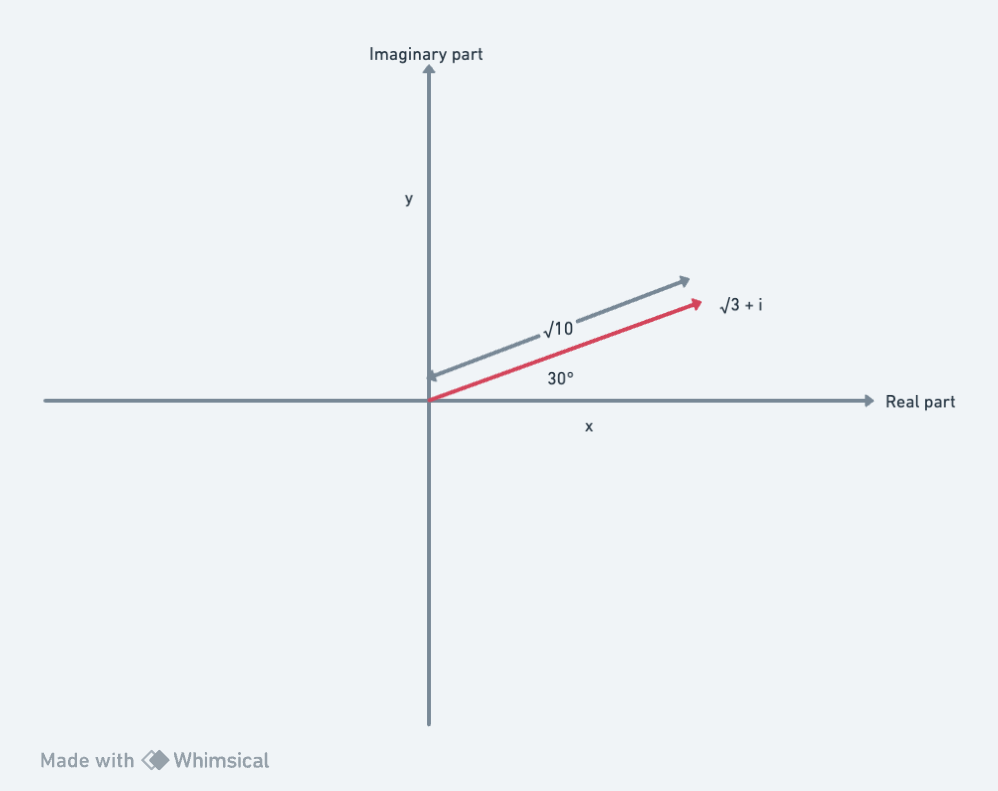
\[\sqrt{3} + i\]

First, we’ll work out the modulus

\[|\sqrt{3} + i| = \sqrt{1^2 + 3^2} = \sqrt{10}\]

Now we’ll work out the argument

\[arg(\sqrt{3} + i) = tan^{-1}(1/\sqrt{3}) = 30^{\circ}\]

So plotting this gives:

Negative arguments

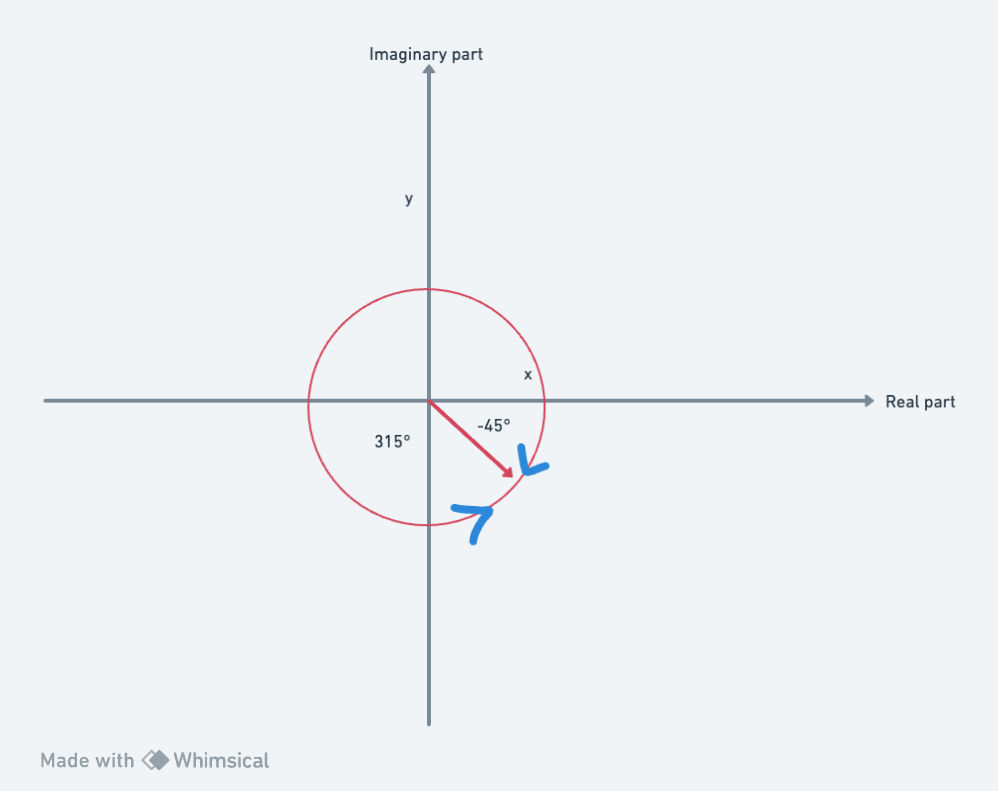
So far we’ve used the anti-clockwise angle from the positive x axis but sometimes it is easier to use the clockwise angle. If we want to use the clockwise angle all we have to do is make it negative.

So the following two numbers are the same (3, 315) and (3, -45) as we can see in this diagram

Euler’s Formula

One of the most famous formulas in mathematics is that

\[e^{it} = cos(t) + isin(t)\]

This identity is called Euler’s formula and using it we can any complex number in the following form

\[r(cos(t) + i sin(t)) = re^{it}\]

This is a really helpful form to write a complex number in as it makes it easy to see what the modulus is which is often important in Quantum Computing.

It also makes multiplying two complex numbers really easy as:

\[r_1e^{it_1} * r_2e^{it_2} = r_1r_2^{i(t_1+t_2)}\]

The other thing it makes easy is taking the complex conjugate as all we have to do is make the angle negative

\[\overline{re^{it}} = re^{-it}\]