Basic Mathematics For Quantum Mechanics - Complex Numbers

The name complex numbers is misleading since complex numbers are not complex at all - so let’s dive in.

What are Imaginary Numbers?

In school, you were told that you cannot take the square root of negative numbers, in fact, you can.

Let’s start with the square root of -1 which is called i so:

\[\sqrt{-1} = i\]

or equivalently

\[i^2 = -1\]

Using this we can work out the square roots of other negative numbers, for example:

\[\sqrt{-4} = \sqrt{4}\sqrt{-1} = 2i\]

So we take the square root as normal and add i on the end.

These numbers of the form ai where a is a real number, are called imaginary numbers.

Complex Numbers

Now we have imaginary numbers we can build complex numbers out of them. We do this by considering numbers of the form

\[a + bi\]

where a and b are real numbers (and can be positive or negative). For example:

\[2 + 3i, 7+12i, 6 - 13i\]

The first part is called the real part and the second part is called the imaginary part.

Visualing Complex Numbers

So far this probably seems very abstract. Thankfully, there is a nice way to visualise complex numbers that makes understanding them much easier.

What we do is we plot them on a diagram where we plot the real part of the x axis and the imaginary part on the y axis

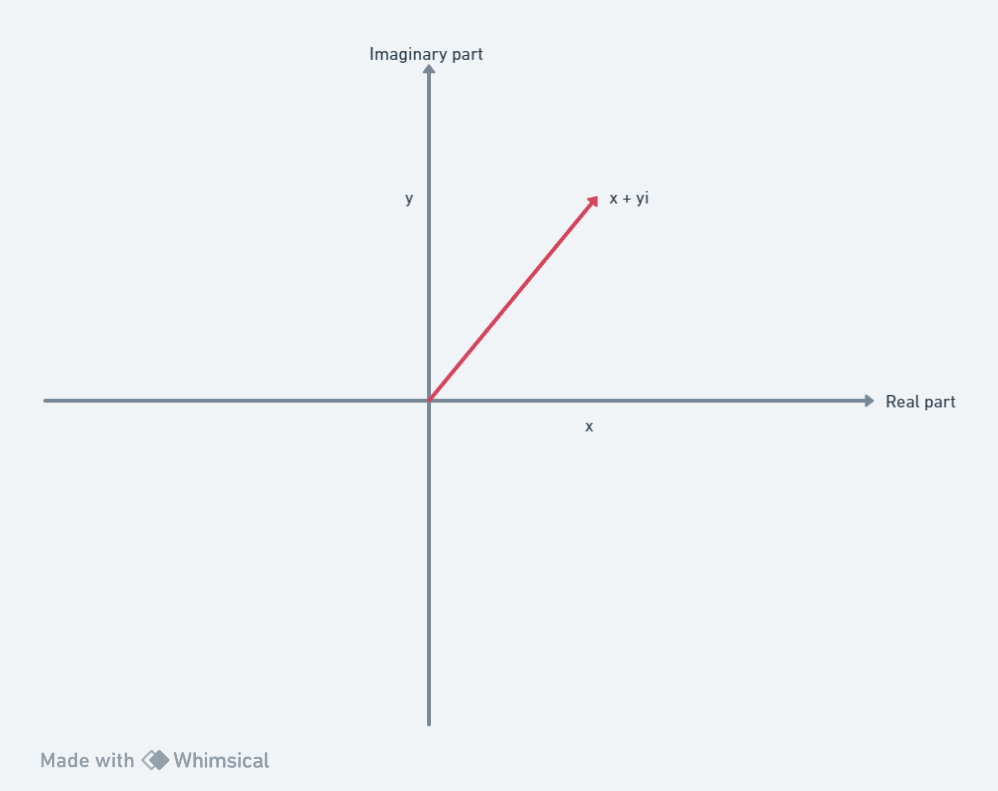
Let’s take a look at 2 + 3i and 2 - 3i when we plot them on this diagram

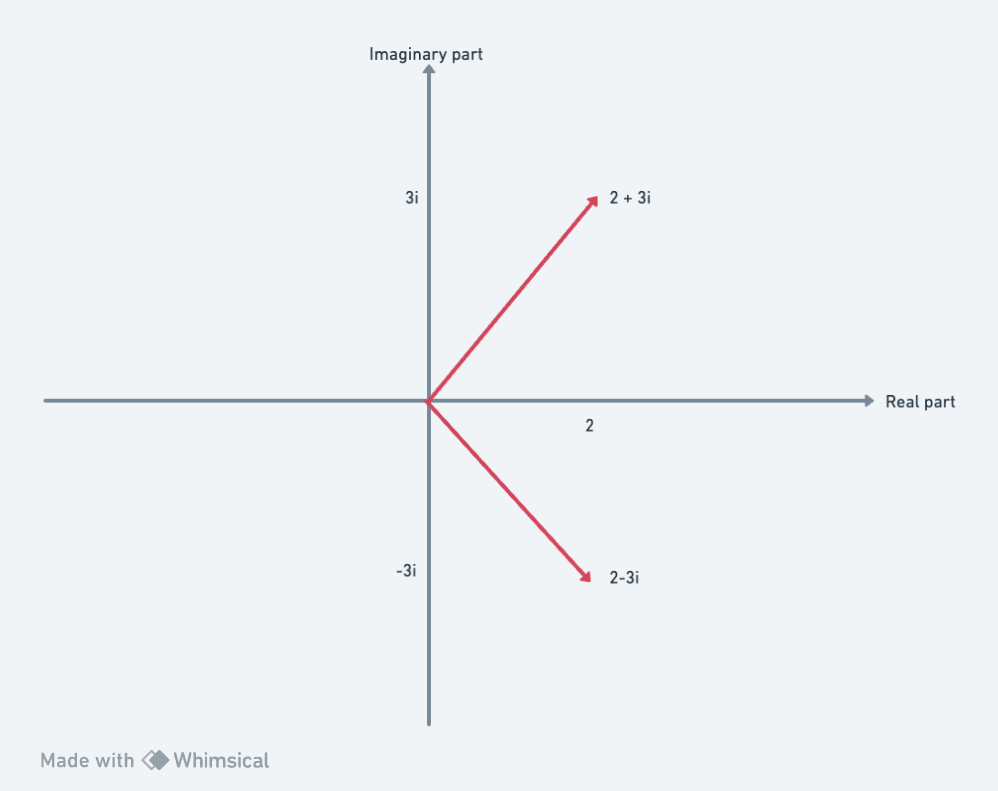
Conjugation

Conjugation is a simple operation - it just means flipping the sign of the imaginary part of a complex number. So a + bi goes to a - bi.

We denote the conjugate of a number by putting a bar over the top of it

Here are some examples:

\[\overline{2 + 3i} = 2 - 3i\] \[\overline{4 - 7i} = 4 + 7i\]

Addition and Subtraction

We can add two complex numbers together. We do this by adding the real parts and imaginary parts separately:

\[(1 + 3i) + (4 + 7i) = (1 + 4) + (3 + 7)i = 5 + 10i\]

Subtraction works in a similar way:

\[(1 + 3i) - (4 + 7i) = (1-4) + (4-7)i = -3 - 4i\]

Multiplication

Multiplying out complex numbers works like expanding brackets in high school algebra:

\[(1 + 3i)(4 + 7i) = 1(4 + 7i) + 3i(4 + 7i) = 4 + 7i + 12i + 21i^2\]

From here we can simplify this using the identity:

\[i^2 = -1\]

So we get

\[(1 + 3i)(4 + 7i) = 4 + 7i + 12i - 21 = -17 + 19i\]

Division

We want to be able to divide two complex numbers. But let us start with something a little simpler: dividing a complex number by a real number.

The rule for doing this is:

\[(a + bi) / c = (a/c) + (b/c)i\]

An example is

\[(9 + 3i)/3 = 3 + i\]

So now we can turn to dividing complex numbers:

\[\frac{a + bi}{c + di}\]

We can turn this into what we already know how to do: multiplying by a complex number and then dividing by a real number. To do this we multiply the top and bottom of the fraction by the complex conjugate of the bottom.

\[\frac{a + bi}{c + di} = \frac{(a + bi)(c - di)}{(c + di)(c - di)} = \frac{(a + bi)(c - di)}{c^2 + d^2}\]

We can do this since we know how to multiply complex numbers together and we know how to divide a complex number by a real number.

Let’s take a look at an example:

\[\frac{1 + 3i}{4 + 7i} = \frac{(1 + 3i)(4 - 7i)}{(4 + 7i)(4-7i)} = \frac{25 + 5i}{16 + 49} = \frac{25 + 5i}{65} = \frac{5 + i}{13}\]

And that’s all we need to know about complex numbers for now. We’ll pick up a bit more in the next post.